前置知识
存图方式(邻接表,邻接矩阵),并查集。
不会的快进入链接学习吧!
引入
生成树,就是从一个图中选中n−1条边,使得这些边构成一棵树,并包含图中的所有节点。
最小生成树,就是找到一种生成树,使得这个生成树的边权和最小。
生成方式一:prim
这种方法有点类似Dijstra,就是每次从所有vis过的点遍历能达到的边,从其中选择一条最小的,加入生成树。
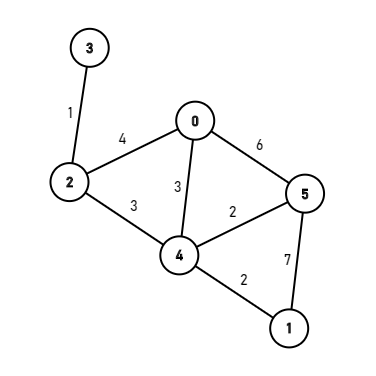
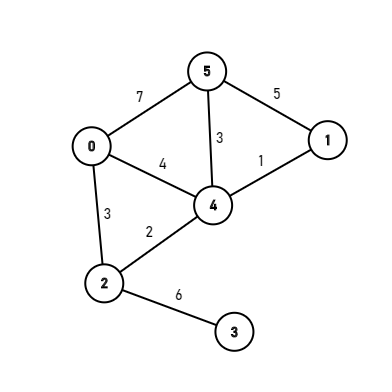
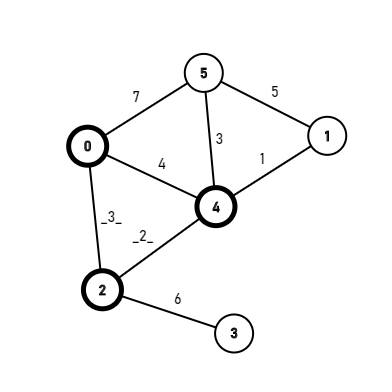
假设我们有这么一张图:
![]()
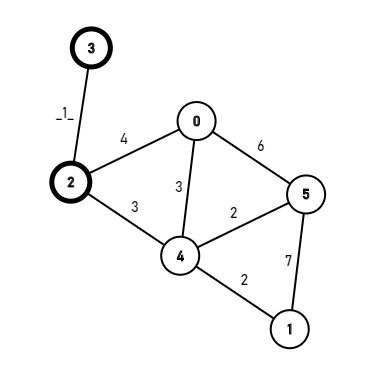
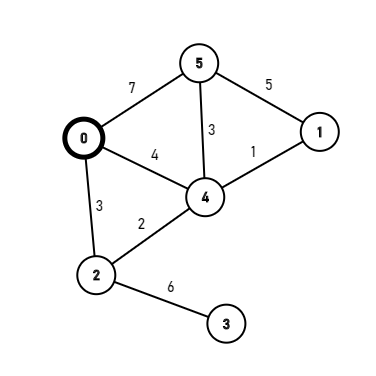
就从0号点开始吧:
![在这里插入图片描述]()
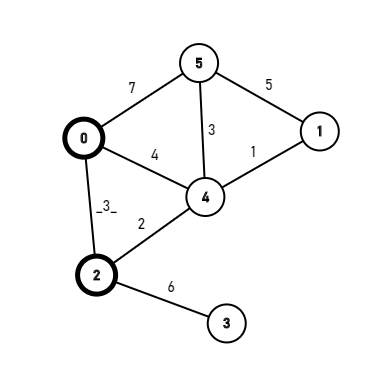
找到从0出发的最小的边:[0,2],边权为3,那么对2号点进行标记。
![]()
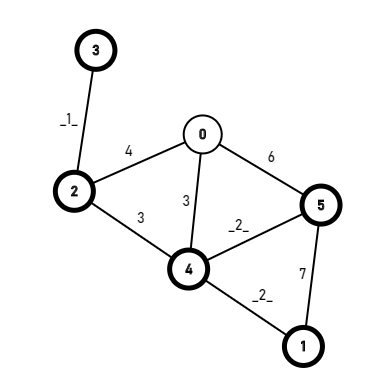
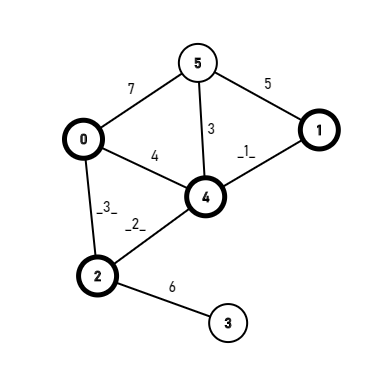
然后从0号和2号节点继续找,发现最小的是[2,4]边,那么就标记4号节点。
![在这里插入图片描述]()
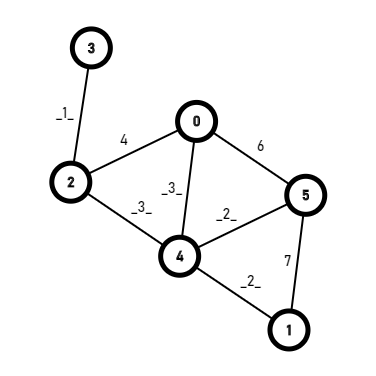
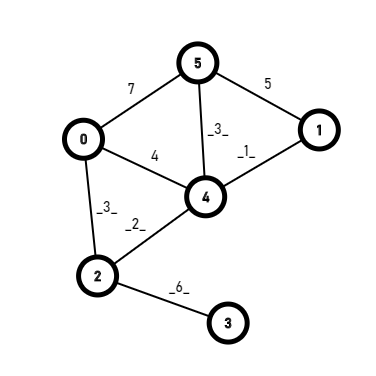
然后是[4,1],1号。
![在这里插入图片描述]()
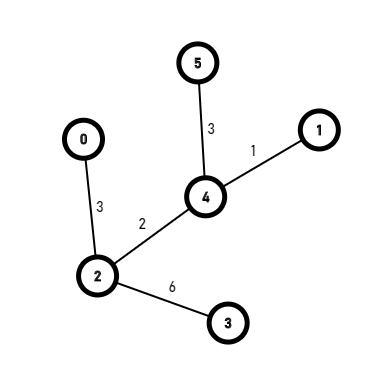
以此类推,最后就生成出来了这样一个图:
![在这里插入图片描述]()
把没有标记的边删掉,就是最小生成树。
![]()
这就是prim算法 ,代码我不会写在后面。
生成方式二:kruskal
这个算法本质上就是把所有边按照边权排序,然后直接爆炸按顺序判断要不要加进生成树里。
kruskal算法使用了一种极速闪电致命又自杀的东西:并查集。
他有多快呢?
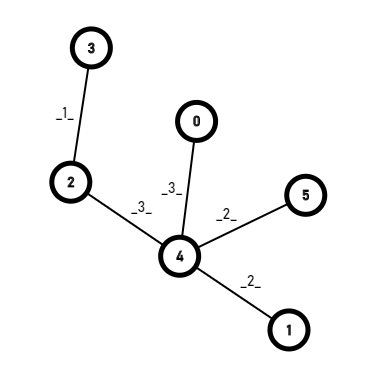
好了我们在建一个图模拟一下吧
![在这里插入图片描述]()
先给边排序。最小的是[2,3],把他拿出来,判断一下。怎么判断呢?首先访问一下并查集看一看,这个边连接的两个点在不在同一个集合内,不在的话就把这条边加入生成树,然后把两个点合并。否则忽略这一条变,继续。这一条边符合要求,加进并查集里,现在2,3是一个集合,剩下都是独立的。
![在这里插入图片描述]()
现在最小的有[1,4]和[4,5],我们都判断一下,都可以。
![在这里插入图片描述]()
然后就是[0,4]和[2,4],依然都是可以的。
![在这里插入图片描述]()
这样,一颗活灵活现的生成树就出现了。
![]()
好了!
kruskal的代码又短又易于理解,甚至可以直接用数组存边,所以他非常好写,推荐。
prim
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
| #include "iostream"
#include "queue"
#include "cstring"
using namespace std;
#define maxm 5000010
#define maxn 1000010
#define inf 0x3f3f3f3f
int ans=0;
struct node{
int v,next,c;
}e[maxm<<1];
int h[maxn],tot,n,m;
void adde(int u,int v,int c){
tot++;
e[tot].v=v;
e[tot].c=c;
e[tot].next=h[u];
h[u]=tot;
}
int dis[maxn];
bool vis[maxn];
struct qu{
int id,dis;
bool operator < (const qu t)const{
return dis>t.dis;
}
};
priority_queue<qu> q;
void dijk(int s){
memset(dis,0x3f,sizeof(dis));
memset(vis,0,sizeof(vis));
while(!q.empty())q.pop();
qu t;
t.dis=0;
t.id=s;
dis[s]=0;
q.push(t);
while(!q.empty()){
t=q.top();q.pop();
if(vis[t.id])continue;
vis[t.id]=true;
ans+=t.dis;
for(int j=h[t.id];j;j=e[j].next){
int v=e[j].v;
if(!vis[v]&&dis[v]>e[j].c){
dis[v]=e[j].c;
qu now;
now.id=v;
now.dis=dis[v];
q.push(now);
}
}
}
}
int main(){
int s=1;
cin>>n>>m;
int u,v,c;
for(int i=1;i<=m;i++){
cin>>u>>v>>c;
adde(u,v,c);
adde(v,u,c);
}
dijk(s);
cout<<ans<<endl;
return 0;
}
|
kruskal
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| #include "iostream"
#include "algorithm"
using namespace std;
int n,m,tot,sum,f[5001];
struct node{
int u,v,c;
}a[200010];
int cmp(const node &u,const node &v){
return u.c<v.c;
}
int getf(int u){
if(f[u]==u)return u;
return f[u]=getf(f[u]);
}
int main(){
cin>>n>>m;
if(m<n-1){cout<<"orz"<<endl;return 0;}
for(int i=1;i<=m;i++)cin>>a[i].u>>a[i].v>>a[i].c;
for(int i=1;i<=n;i++)f[i]=i;
sort(a+1,a+m+1,cmp);
for(int i=1;i<=m;i++){
int fu=getf(a[i].u),fv=getf(a[i].v);
if(fu!=fv){
f[fu]=fv;
sum++;
tot+=a[i].c;
}
if(sum==n-1)break;
}
cout<<tot<<endl;
}
|