\(P+Q=-R\)

背景:Alice 想要发布带数字签名的消息(文件、游戏、应用程序等等)。只有 Alice 能产生合法的数字签名,但所有人都应能验证数字签名是否合法。
Alice 打算使用 ECDSA 算法,首先需要一个定义在椭圆曲线上的群。
椭圆曲线是这样的点集:\(\left\{(x,y)\in\mathbb{R}^2\ |\ y^2=x^3+ax+b,4a^3+27b^2\ne0\right\}\cup\left\{0\right\}\)。其中 0 是无限远处的点。
我们需要的群定义如下:
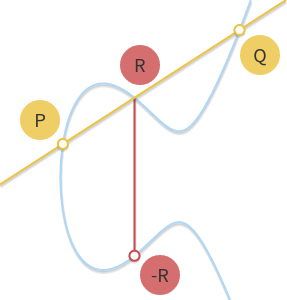
当然在计算机上不能用几何方法计算这个加法,还需要代数方法。
首先需要知道直线的斜率 \(m\)。若 \(P,Q\) 不同且非 0,可得 \(m=\dfrac{y_P-y_Q}{x_P-x_Q}\)。若 \(P=Q\),则需要切线斜率 \(m=\dfrac{3x_P^2+a}{2y_P}\)。
通过解三次方程,得出 \(R:(m^2-x_P-x_Q,y_P+m(x_R-x_P))\)。
有了计算机可以简单计算的加法后,接下来定义数乘:\(nP=\underbrace{P+P+\cdots+P}_{n\ \text{times}}\)。
加入快速幂思想,我们就知道给定 \(n,P\) 计算 \(Q=nP\) 是容易的。但如果要从 \(P,Q\) 计算 \(n\) 呢?
这里就要说到密码学里不得不提的“离散对数”问题。这说的是在模素数的非负整数域上,计算对数是困难的。
我们也要制造类似的困难,那么就要把定义域也变为离散的(\(p\) 是素数):\(\left\{(x,y)\in\left(\mathbb{F}_p\right)^2\ |\ y^2\equiv x^3+ax+b\pmod{p},4a^3+27b^2\not\equiv 0\pmod{p}\right\}\cup\left\{0\right\}\)
为了保留加法的定义,我们将直线改为 \(ax+by+c\equiv 0\pmod{p}\),视觉上表现为从定义域的上方穿透到下方,循环往复的直线。
那么刚才的公式依然可用,只是需要将除法改为乘法逆元,如 \(m=(y_P-y_Q)(x_P-x_Q)^{-1}\bmod{p}\),以此类推。
由此,给定 \(n,P\) 计算 \(Q=nP\) 依然是容易的。但目前认为,椭圆曲线上的“离散对数”,即从 \(P,Q\) 计算 \(n\),是比 RSA 所用的分解素数问题更为困难的。
不过,这一困难还需要子群的阶足够大以作为担保。
可以证明,以任意 \(P\) 作为生成元,所生成的(即 \(P\) 的所有倍数)一定是个循环子群。
根据拉格朗日引理,这个循环子群的阶 \(P\) 一定是整个群的阶 \(N\) 的因数。所以,我们只需要先计算 \(N\),对于它从小到大的每个因数 \(n\),计算 \(nP\),直到 \(nP=0\) 时得到的就是这个子群的阶。
但我们不会一个一个试出最好、最大的阶,而是直接选取子群的阶,再由此确定生成元。这一方便还要归功于拉格朗日引理。
首先还是计算 \(N\),找到一个它的质因数 \(n\)。我们知道对于任意点 \(P\) 都满足 \(NP=0\),也就是 \(n(\dfrac{N}{n}P)=0\),根据拉格朗日引理可知 \(\dfrac{N}{n}\) 也是个整数,这实际上就是说点 \(G=\dfrac{N}{n}P\) 能生成一个阶为 \(n\) 的子群。
如此这般,我们从 \(1\dots n-1\) 中随机选取一个数 \(d\) 作为私钥,将 \(H=dG\) 作为公钥,就得到了椭圆曲线加密算法。
好了,现在我们有了这一极好的算法,可以用它来做数字签名了:
其他人要验证签名是否合法时:
证明:\(u_1G+u_2H_A=(u_1+u_2d_A)G=(s^{-1}h+s^{-1}x_Pd_A)=s^{-1}(h+x_Pd_A)G=kG\)。
你可以在下方生成自己的数字签名。这样封装起来,这个算法似乎又变得非常简单了。世界上更多算法又何尝不是这样呢,看似简单,其实背后有着数论、群论,几何、代数等等多领域的结合。只有深入到其原理,才能看清这些算法的复杂之处。
关于椭圆曲线加密算法,需先阅读 ECDSA 的介绍。