并查集

前置知识

哈哈，简单到爆，没有。 ### 引入 并查集是一种快到爆炸的集合算法，可以进行两项基本操作：合并两个集合（并）、查询两个参数是否在一个集合内（查）。这也是它名字的由来。 ### 速度 他有多快呢？ $O(*log n)$ $*log$有多可怕： |$n$|$*log n$| |-|-| |$(1,2]$|$1$| |$(2,4]$|$2$| |$(4,16]$|$3$| |$(16,65536]$|$4$| |$(65536,2^{65536}]$|$5$| 所以n是$2^{65536}$的时候复杂度还只有5。 $2^{65536}$有多大，我把他拷进来的时候整个电脑卡死了。我不得不强制重启，然后重新写一遍这段。他有19729位。想通了吧？ ### 如何实现 这么高端的算法，是怎么实现的呢？ 其实

它的本质就是一个数组$f[]$，和一个函数$getf()$ $f[]$存的实际上就是几棵树。 $f[i]$就是$i$的父亲。 $getf(i)$做的操作就是递归顺着$f[i]$找$i$所在的树的根。 $getf()$代码：

int getf(int x){
	if(f[x]==x)return x;
	else return getf(f[x]);
}

$...$

那这个算法就很低端了$...$

那还讲个鬼啊$...$

所以 ### 超级优化 我们首先随机造出一些操作：

10
merge 1 5
merge 5 2
merge 1 3
check 2 3
merge 3 4
merge 6 7
check 1 7
merge 7 8
merge 8 9
merge 1 9
check 7 4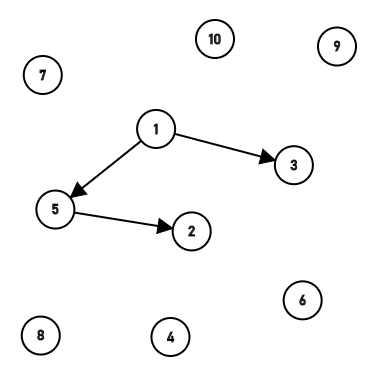

其中，merge代表合并，check代表查询。 如果按照刚才所的算法，那么在第一次查询之前，就会出来这样的森林： 到最后，就形成了这样一个繁杂的森林，要找到一个点的根，就需要走很长一段路。这就拉长了时间。 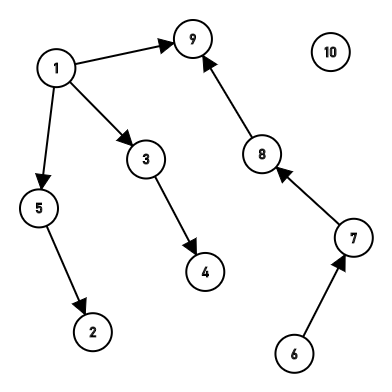为了缩减时间，超级优化就出现了：路径压缩。 路径压缩其实也很简单：在$getf()$查找根节点的同时，把自己也链接到根节点上，使得树的深度不超过2。 代码：

int getf(int x){
	if(f[x]==x)return x;
	else return f[x]=getf(f[x]);
}

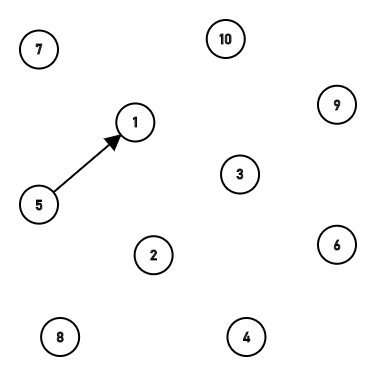发现没有，和之前的代码相比，只改了一个地方，就让时间大大压缩。 这时我们在模拟一下。 第一次合并： 第二次合并时，首先寻找2,5两个节点的根节点，2的根就是2，5的根是1，于是直接把2链接到1上。 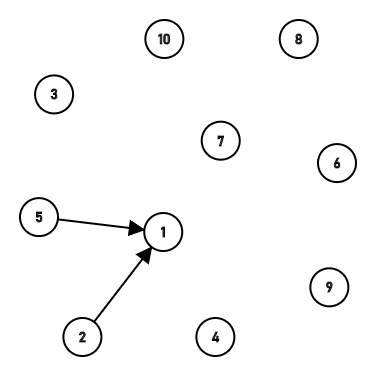第三次，第四次合并把3链接到了1上，然后把4顺着3也链接到了1上，第五次连接了6和7。 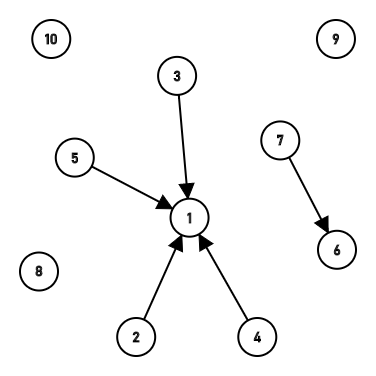第七次第八次链接成了$9\rightarrow8\rightarrow7\rightarrow6$一长串，然后经过路径压缩都链接到6上了。 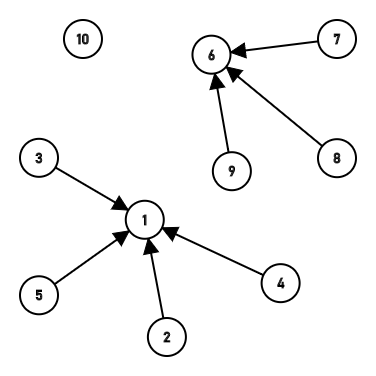最后一次，把9和1链接起来了，这时深度又超过了2，一下还压缩不下去，不过没关系，查询的时候就会把它压缩的。 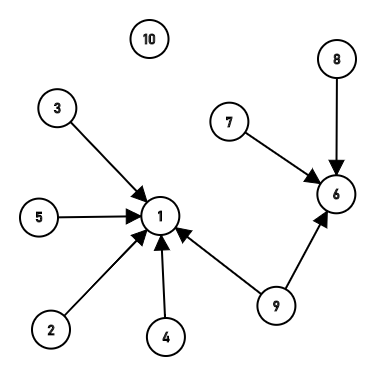比如查询7和4的时候就会分别寻找7和4的根节点，一路递归找上去的时候就直接把路径压缩好了，除了8还链接在6上，其他全部链接到1上了。 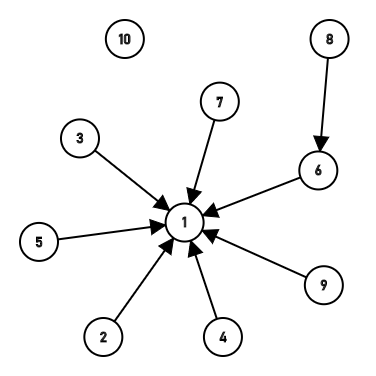多么有趣啊！ ### 代码 自己想去吧，核心代码和思路都给出来了。 有一个巨大的坑，就是$f[i]$要预设成$i$，不然会爆炸。 加油！克服恐惧的最好办法就是面对恐忄快去写吧！